fed-GLMM
Developed a federated learning framework on GLMM
This project developed federated solutions based on two approximation algorithms to achieve federated generalized linear mixed effect models (GLMM).
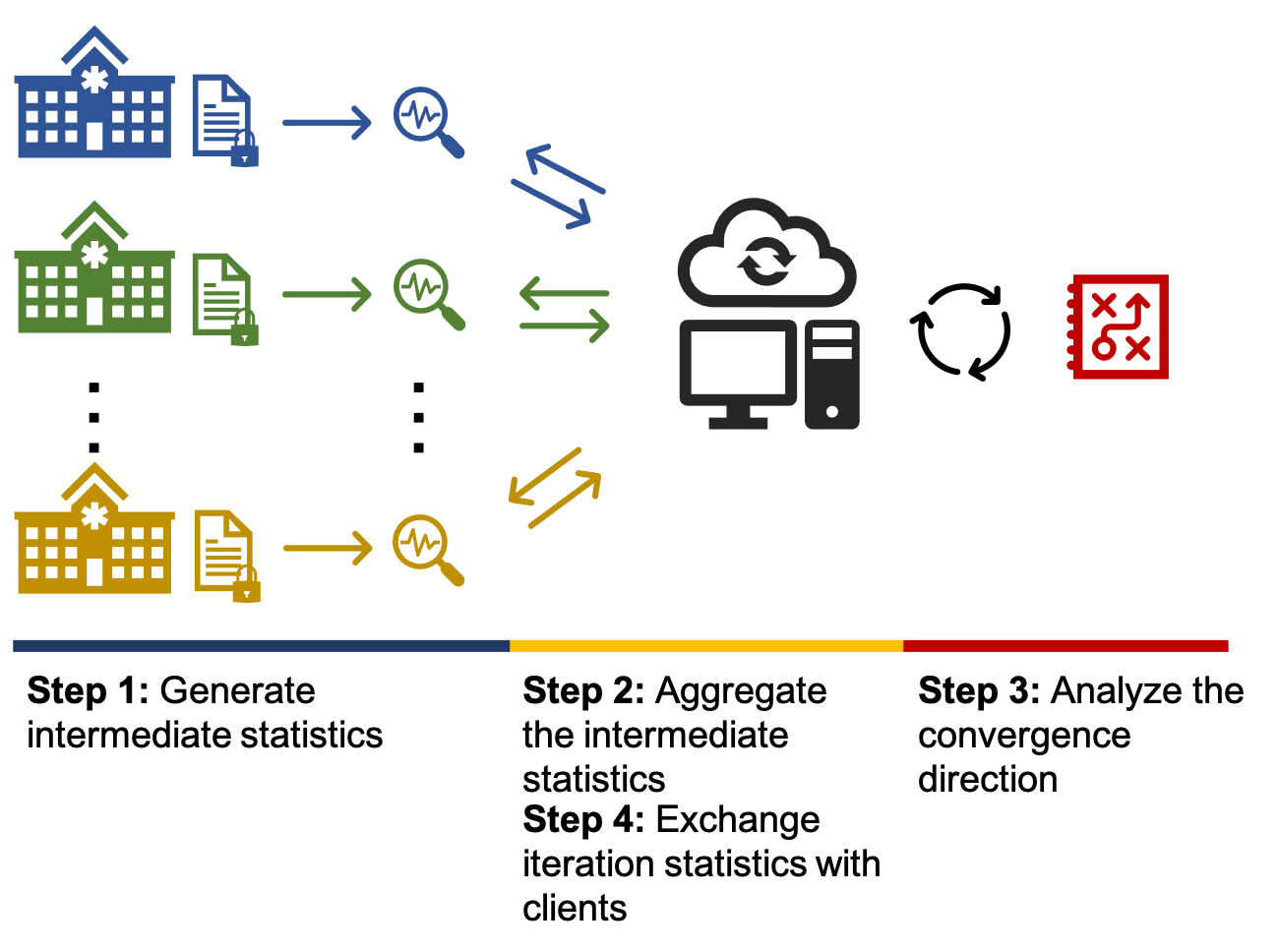
This schema of federated learning model shows collaborative data analsyis among geographically distributed healthcare institutions. The local institutions periodically exchange intermediate statistics and update the convergence situation of the global model.
In this project, I solved the mathematical intractable problem with two approxiamtion methods: Laplace and Guass-Hermite. And the intractable log-likelihood function is defined as
\[\log\{\mathcal L(\theta)\}=\sum_{i=1}^{m}\log\left\{\int_{\mu_{i}}\left[\prod_{j=1}^{n_i}\mathbb P(\theta|X_{ij},y_{ij})\right]\phi(\mu_{i};\tau)\text{d}\mu_{i}\right\}\]The convergence of the approximation of the likelihood function may be compromised due to over-fitting. Also, for those spatially correlated data, the convergence of them may lead to a complex model. Hence, I also added an \(L2\) regularization is added to the local log-likelihood function of Gauss-Hermite approximation form, and as shown below
\[l_i=\log\mathcal L_i=\log\left(\sqrt{2\pi}\hat\omega\sum_{k=1}^Kh_k\exp\left\{g(\hat\mu_{i}+\sqrt{2\pi}\hat\omega x_k;\theta)+x_k^2\right\}\right) - \lambda\|\beta\|^2_2\]Results visualization
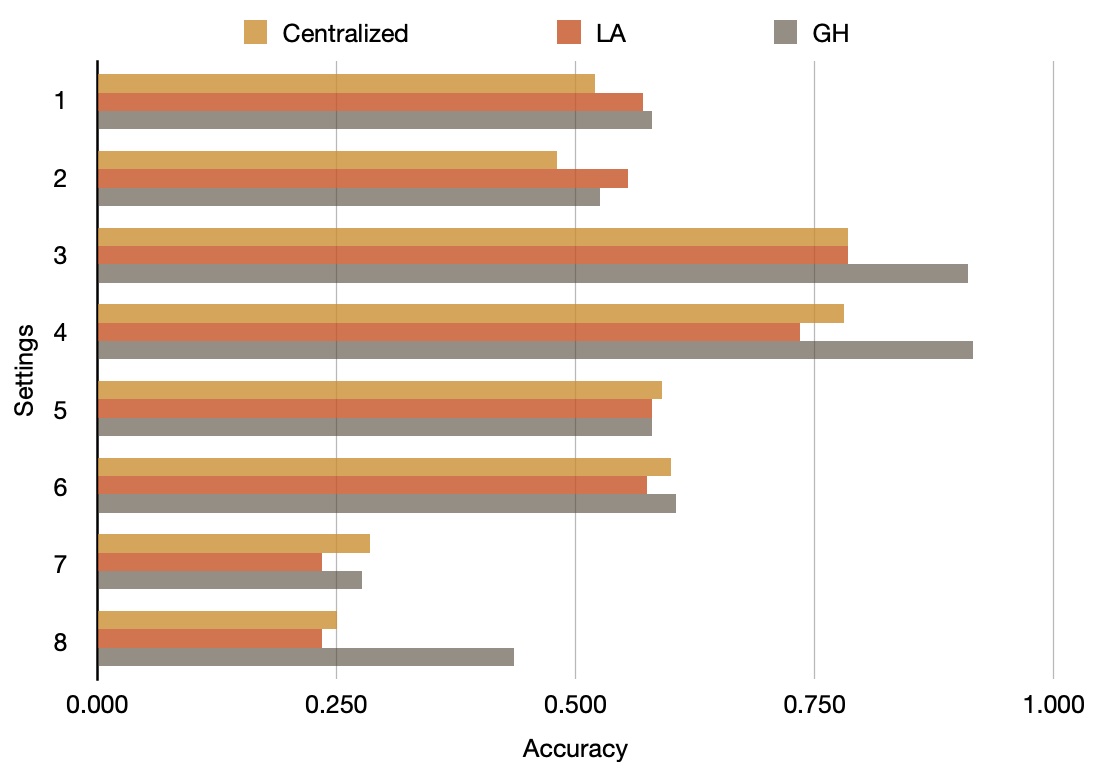
We can see that the federated GH method outperformed the Centralized LA and the federated LA methods, thanks to its better approximation using higher-degree functions. Here, we use the true parameters and their p-values set during the data the synthetic data generation process as the golden standard. The accuracy means the alignment ratio of three different methods against the gold standard.
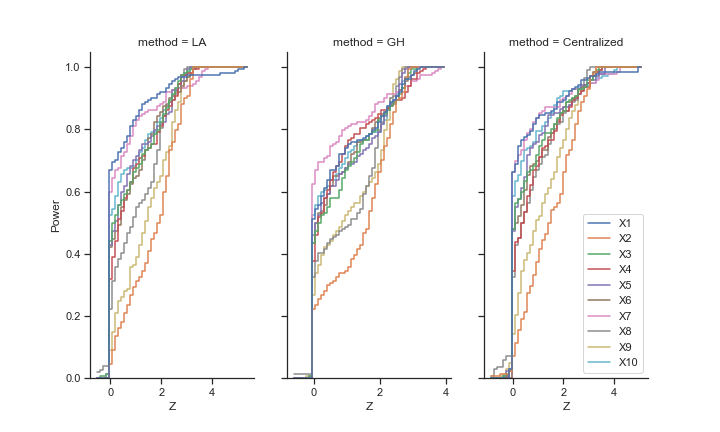
Also, notice that the federated Gauss-Hermite method achieved higher test power.